Quantum Reinforcement Learning Gets an Entanglement Boost Using Single Photons

In this work, we have demonstrated a novel approach to quantum reinforcement learning that harnesses the power of entanglement using single photons. This breakthrough could pave the way for more efficient learning algorithms in quantum computing applications for specific tasks by exploiting the intrinsic communication that entanglement offers.

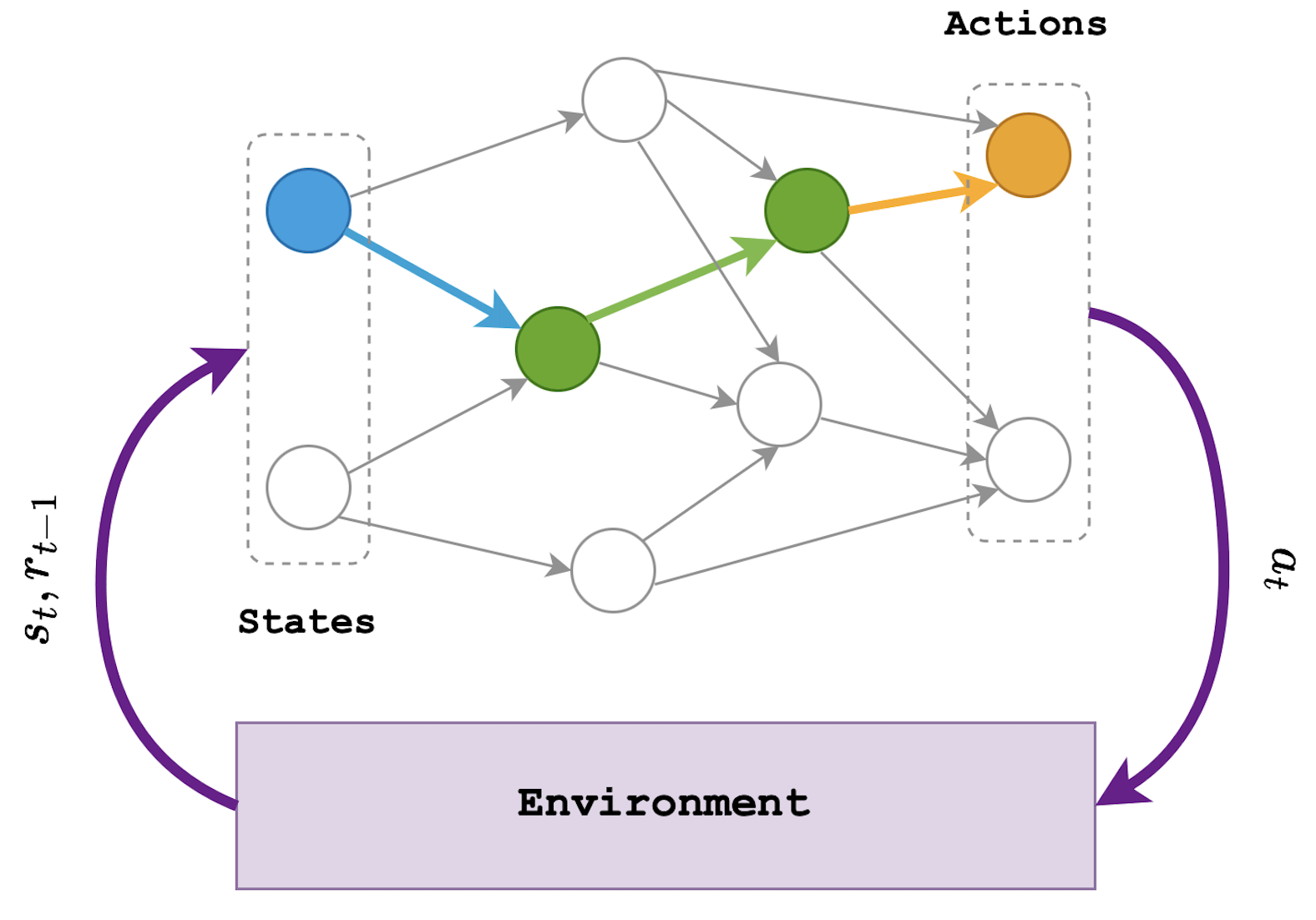
Figure 1: In reinforcement learning we have an agent that interacts with its environment. The agent receives the current state of the environment (stimulus) based on which it performs an action that affects the envornment. Depending on the quality of the performed action, it receives a reward (positive or negative).

What is reinforcement learning ?

Reinforcement learning (RL) is a type of machine learning where agents learn through trial and error by interacting with their environment. While classical RL has shown impressive results, quantum reinforcement learning (QRL) promises to enhance this further by leveraging quantum mechanical properties like superposition, entanglement, and interference.

The Innovation: Quantum Optical Projective Simulation (QOPS)

At Quandela, we have developed a framework called Quantum Optical Projective Simulation (QOPS), which is based on a classical machine learning method called Projective Simulation (PS). Here’s what makes it special:

1. Interpretable learning: Unlike “black box” approaches like neural networks, QOPS makes the learning process more interpretable by using a structure called Episodic Compositional Memory (ECM).
2. Quantum enhancement: The framework uses quantum walks of single photons through optical circuits, instead of random walks in graphs, taking advantage of quantum properties like superposition and interference to potentially speed up learning.
3. Entanglement boost: For the first time, entanglement is incorporated into the PS framework, leading to improved performance in certain scenarios.

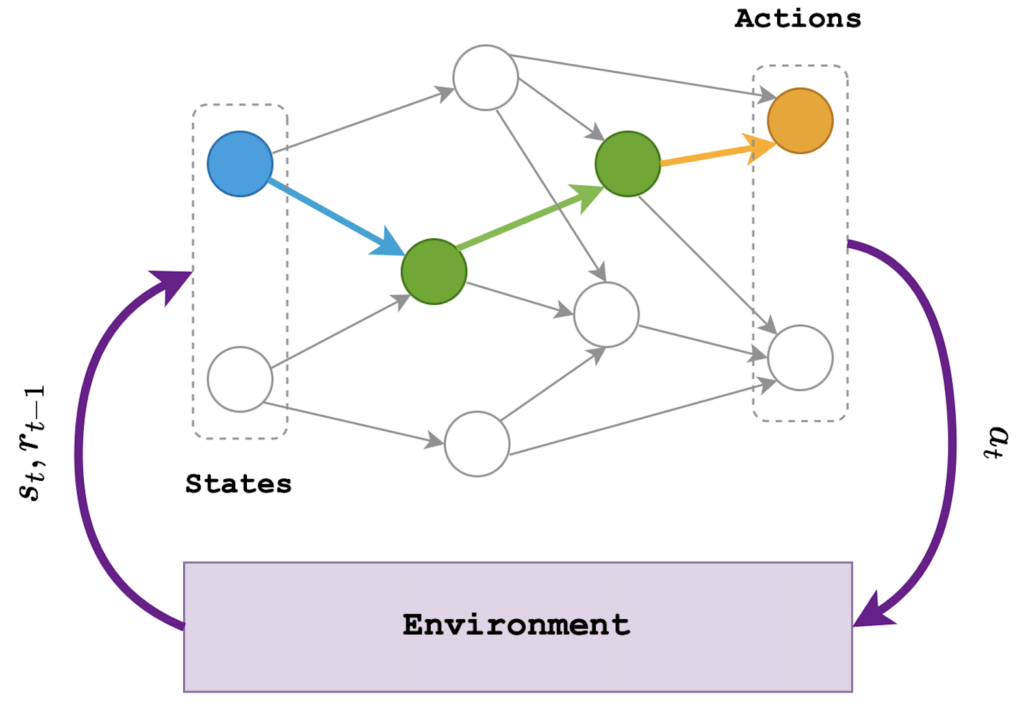
Figure 2: The projective simulation framework uses Episodic Compositional Memories (ECM) to enhance the interpretability of RL models. Classically, the decision process in ECMs is modelled by performing a random walk in the graph. Quantumly, using photonics, the same procedure is modelled by a photon walk in a quantum optical circuit.

Application on the prisoner’s Dilemma

To demonstrate our framework, we implemented a quantum version of the famous Prisoner’s Dilemma game. In the classical world, Prisoner’s Dilemma is a game theory concept illustrating the tension between individual rationality and collective benefit. Two prisoners must independently choose to cooperate (stay silent) or defect (betray). Mutual cooperation yields a moderate sentence, but if one defects while the other cooperates, the defector goes free while the cooperator receives a harsh sentence. If both defect, they get a severe sentence. Since defection is the dominant strategy, both acting in self-interest leads to a worse outcome than cooperation, highlighting key challenges in trust and strategic decision-making.

• Two players must decide whether to cooperate or defect.
• The decisions are made using quantum strategies.
• The system uses entangled photons to enhance decision-making.

Key Technical Achievements

To implement the idea of entangled QOPS for a specific use case and demonstrate the advantages of quantum properties, we had to deal with several challenges requiring the development of innovative methods:

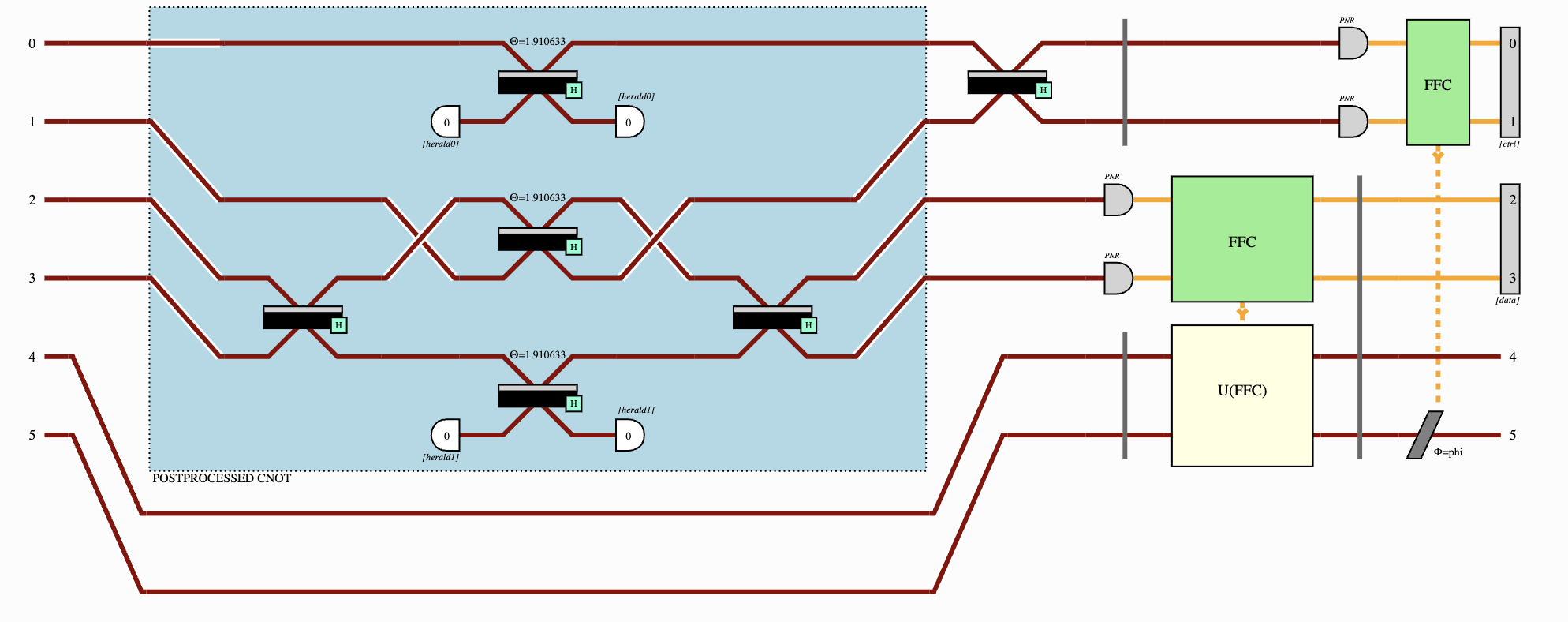
1. Efficient translation: Development of an efficient method to convert any 2-layer ECM into a quantum optical circuit, making it practical for implementation on real quantum hardware.
2. Noise resistance: The framework showed promising results even in the presence of noise, making it suitable for current-generation (NISQ) quantum computers.
3. Possibility of efficient implementation on real QPU: The system was tested using Altair’s noisy simulator, which emulates Quandela’s real single-photon quantum processor, providing promising results.

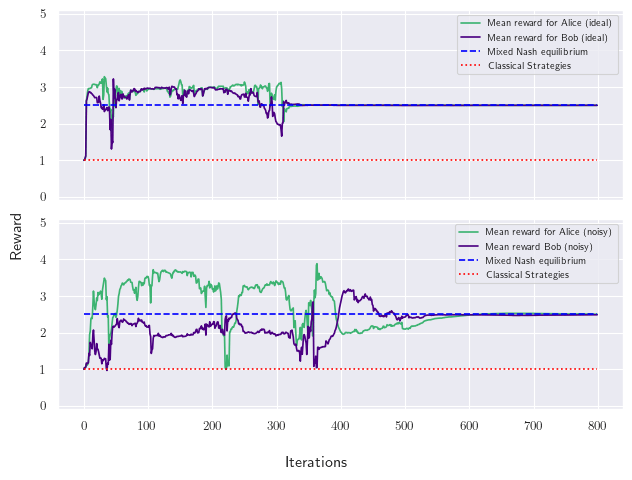
Figure 3: In game theory the goal is to approximate the reward values that correspond to the Nash Equilibrium (blue dashed lines). However, using classical methods, the max reward values the players can achieve is lower (red dashed line). Using quantum methods, we are able to converge to the reward values of the Nash Equilibrium. Moreover, the results from the noisy simulator and the comparison to the ideal one verify that the model remains robust even in the presence of noise.

Practical Applications

The framework shows promise for several real-world applications related to the Prisoner’s Dilemma and requiring optimal decision-making. Some examples include:

1. Drone navigation: Could help optimize multiple drone trajectories while avoiding collisions in shared airspace, exploiting the intrinsic communication that entanglement offers.
2. Strategic decision-making: Useful for scenarios where multiple agents need to make cooperative or competitive decisions.
3. Quantum game theory: Provides new insights into how quantum mechanics can enhance strategic decision-making.

Why is this work important?

This research is significant because it:

1. Bridges the gap between theory and practice: Demonstrates how theoretical work can be implemented on real quantum hardware.
2. Noise-resilient algorithm: The framework is designed to work with current NISQ (Noisy Intermediate-Scale Quantum) devices.
3. Expands quantum computing applications: Opens up possibilities for quantum-enhanced learning in various fields, from robotics to economics.

What comes next?

The milestones achieved in this work are important, but there is always room for improvement. That’s why we have already identified several promising directions for future work:

• Hardware implementation: Run the algorithm on actual quantum processors (currently in progress on Quandela’s photonic quantum processor).
• Direct entanglement: Generate entangled states directly from Single Photon Sources (SPS) to improve circuit performance.
• Real-world applications: Scale the approach for use in real-world problems like drone navigation or multi-agent systems. This is the most challenging step due to the resource requirements needed to increase the problem size (i.e., number of agents).

Impact on the Field

This work represents a step forward in making quantum reinforcement learning practical. By demonstrating that quantum-enhanced learning can work even in noisy environments, it brings us closer to realizing the potential advantages of quantum computing in machine learning applications.

The combination of interpretability, noise resistance, and the novel use of entanglement makes this framework particularly promising for near-term quantum computing applications.